그래프의 절단점과 절단선 찾기

간선의 분류

절단점과 절단선을 구분하기 위해 먼저 그래프에서 간선을 분류해보자.

스패닝 트리

그래프에서 한 정점을 깊이 우선 탐색했을 때, 탐색이 따라간 간선들만 모아서 보면 트리 형태를 띄는 것을 알 수 있다. 이를 스패닝 트리 라고 부른다.

간선의 분류

이렇게 스패닝 트리를 만들면 그래프의 모든 간선을 네 가지로 분류할 수 있다.

1. Tree edge: 스패닝 트리에 포함된 간선
2. forward edge: 스패닝 트리의 선조에서 자손으로 연결되지만 트리 간선은 아닌 간선
3. back edge: 스패닝 트리의 자손에서 선조로 연결되는 간선
4. cross edge: 위 세가지 분류에 속하지 않는 간선

그렇다면 어떻게 분류할 수 있을까?

1. Tree edge

   dfs(u)내에서 간선 (u, v)를 검사했을 때, v가 방문된 적이 없다면 (u, v)는 트리 간선이다. 

2. 나머지 edge

   dfs(u)내에서 간선 (u, v)를 검사했을 때, v가 이미 방문되었다면 v가 u의 부모인지, 자손인지, 둘 다 아닌지 알 수 없다. 
   따라서 방문 순서를 기록하도록 discovered를 구성해야 한다. 
   이때, 
   1) (u, v)가 forward edge라면 v는 u의 자손이어야 하므로, discovered[v] > discovered[u]
   2) (u, v)가 back edge라면 v는 u의 선조이므로, discovered[v] < discovered[u]
   3) (u, v)가 cross edge라면 dfs(v)가 종료한 후 dfs(u)가 호출되어야 하므로 discovered[v] < discovered[u] 
   
   근데 여기서 문제점은 back과 cross를 구별할 수 가 없다. 따라서 finished라는 배열을 추가로 두어 dfs(v)의 종료 여부를 기록하여 둘을 구분한다. 

code

vector<vector<int>> adj; 
vector<int> discovered, finished; 
int counter = 0;
void dfs(int here) {
  discovored[here] = counter++; 
  for(auto &there:adj[here]) {
    if(discovered[there] == -1) {
      cout << "tree edge" <<endl; 
      dfs(there);
    } else {
      if(discovered[here] < discovered[there])
        cout << "forward edge" << endl;
      else {
        if(!finished[there])
          cout << "back edge" << endl;
        else 
          cout << "cross edge" << endl;
      }
    }
  }
  finished[here] = true; 
}

절단점과 절단선

여기서는 모든 그래프를 무방향 그래프라고 가정합니다.

기억하세요! 무향그래프는 cross edge를 가지지 않습니다.

절단점

가장 간단하게 찾는 방법은 해당 정점을 그래프에서 삭제한 뒤 컴포넌트 개수가 이전보다 늘어났는지를 확인하는 것이다. 하지만 모든 정점에 대해 이 방법을 사용하면 dfs를 |V|번 수행하게 되어 성능이 매우 안좋다.

위에 소개했던 간선의 분류를 통해 한 번의 dfs로 절단점을 찾을 수 있다. 어떻게?

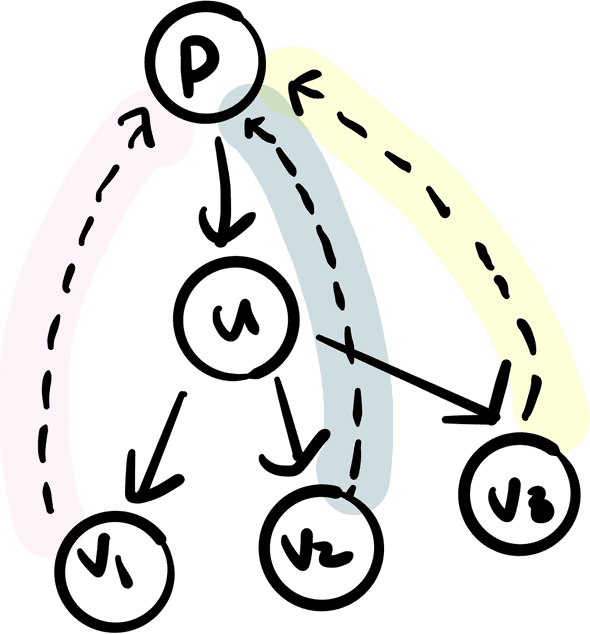
u를 제거했을 때 그래프가 분할될지 어떻게 알 수 있을까 u를 지웠을 때 u의 자손들 (그림에서 v1, v2, v3)가 u의 부모(p)와 연결되는지 확인하면 된다. 즉, u의 자손들이 역방향 간선을 통해 u의 부모로 갈 수 있는지를 파악하면 된다.

가장 쉽게 확인하는 방법은 u 의 서브트리에서 역방향 간선을 통해 갈 수 있는 정점의 최소 깊이를 반환하는 것이다. 만약 u 의 자손들이 모두 역방향 간선을 통해 u 의 선조로 올라갈 수 있다면 u 는 절단점이 아니다.

vector<vector<int>> adj; 
vector<int> discovered;
vector<bool> isCutVertex;
int counter = 0; 

int dfs(int here, bool isRoot) {
  discovered[here] = counter++; 
  int earliestByBackEdge = discovered[here];
  int child = 0;
  for(auto &there:adj[here]) {
    if(discovered[here] == -1) {
      child++;
      int subtree = dfs(there, false);
      if(!isRoot && subtree >= discovered[here]) {
        isCutVertex[here] = true;
      }
      earliestByBackEdge = min(earliestByBackEdge, subtree);
    } else {
      earliestByBackEdge = min(earliestByBackEdge, discovered[there]);
    }
  }
  if(isRoot) 
 		isCutVertex[here] = (child>=2);
  return earliestByBackEdge; 
}

절단선

Bridge라고 부르며, 제거되었을 때 그래프의 컴포넌트 개수가 증가하게 되는 간선을 의미한다.

DFS로 절단선을 찾을 수 있다. 어떻게!

가장 먼저 파악해야하는 점은 절단선은 무조건 Tree edge라는 것이다. 그 이유는 forward edge나 back edge가 있다는 것은 tree edge 가 존재한다는 의미이고 그러면 (u, v)를 연결하는 또 다른 간선이 있다는 의미이기 때문이다.

그럼 이제 문제는 다음과 같다.

Tree edge에서 어떤 특성이 Bridge일까?

단절점과 유사하다. (u, v)를 봤을 때 u에서 부모로 가는 간선을 제외하고 (왜 제외해야하는지는 의문),

v의 subtree가 갈수있는 가장 위의 정점과 비교하여 더 크다면 bridge가 된다.

vector<vector<int>> adj;
vector<int> discovered; 
int counter = 0;

int dfs(int here, int parent = -1) {
  discovered[here] = counter++;
  int earliest = discovered[here];
  for(auto &there:adj[here]) {
    if (there == parent) // edge 여러개인 경우 무시 
      continue; 
    if (discovered[there]==-1) {
      int subtree = dfs(there, here);
      if (subtree > discovered[here])
        IS_BRIDGE(here, there); 
      earliest = min(earliest, subtree);
    } else {
      earliest = min(earliest, discovered[there]);
    }
  }
  return earliest;
}

BOJ 1734 교통체계

풀이

진짜 어렵고 어렵다.

핵심은 a, b가 도대체 어떤 서브 그래프에 속해있는가?

1. a, b, c, d

   (c, d)가 끊어졌을 때, 그래프가 두 부분으로 나뉘어지게 될 것이다. 이 때, a, b가 같은 서브그래프라면 문제 없다. 그런데 이걸 어떻게 판단할까?

   V가 굉장히 크기 때문에 한 번의 dfs로 모든 정보를 저장해 두어야한다.

   • 먼저 절단선인지 아닌지를 판단해보자.

   c가 조상이라고 가정하고 
   1. depth[d]!=depth[c]+1 이면 c, d 사이에 다른 자손 x가 포함되어 있다는 소리이고, 이는 (c, d)가 끊어지더라도 (c, x, d)라는 다른 경로가 생기므로 절단선이 아니다. 
   2. subtree[d] < discovered[d] 이면 d의 자손이 back edge를 가진다는 소리이고 이는 (c, d)가 끊어지더라도 (c, x, d)로 연결될 수 있다. 

   • 절단선이 아닐 때, a, b가 어디로 속하게 되는지 파악해보자.

   절단선이면 c편, d편으로 나누이진다. 따라서 둘의 조상이 같기만하면 (a, b)는 끊어지지 않는다. 

   • 위의 경우가 아니라면 (a, b)는 끊어진다.

2. a, b, c

   정점 c를 제거했을 때 c가 절단점이라면 그래프가 두 개 이상으로 나누어질 것이다. 절단점인지 아닌지 파악하기 전에 a와 b가 c의 조상이라면 c 가 없어도 아무 일도 없다.

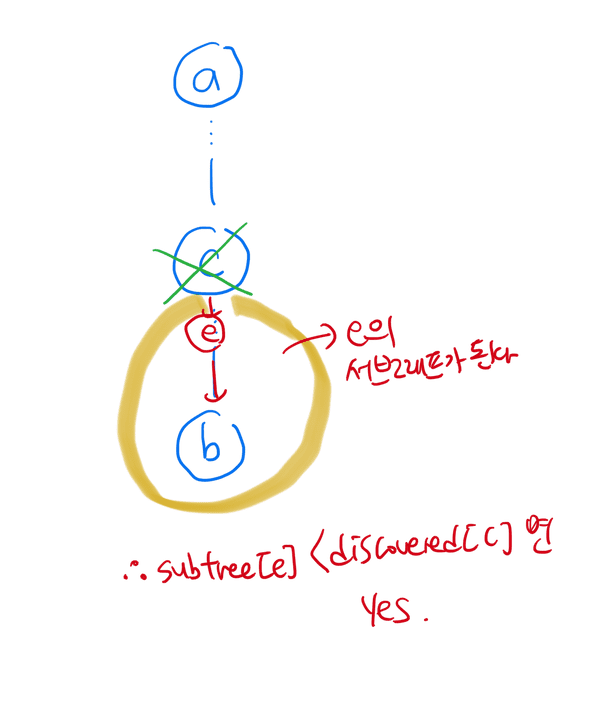
   1. !is_descendant(a, c) && !is_descendant(b, c) 
   2. is_descendant(a, c) && is_descendant(b, c) 
    -> 어디에 속하게 될지 파악하자 
    1) e=find_related_child(c, a) == f=find_related_child(c, b) 
    -> 같은 부분에 속하므로 문제가 없다. 
    2) subtree[e] < discovered[c] && subtree[f] < discovered[c] 
    -> 둘 다 c위의 조상들과 연결되므로 문제가 없다. 
    3) 끊어진다. 
   3. 위의 경우를 모두 제외하고 다른 경우가 있다. 하나는 c의 조상, 하나는 c의 자손일 경우이다. 밑의 그림을 보면 쉽게 이해할 수 있다.