Disjoint Set Union
공통 원소가 없는, 상호 배타적인 부분 집합들로 나누어진 원소들에 대한 정보를 저장하고 조작하는 자료 구조
-
세가지 연산
- 초기화: n개의 원소가 각각의 집합에 포함되어 있도록 초기화
- 합치기(union): 두 원소 a, b가 주어질 때 이들이 속한 두 집합을 하나로 합침
- 찾기(find): 어떤 원소 a가 주어질 때 이 원소가 속한 집합 반환
배열로 상호 배타적 집합 표현하기
가장 간단한 방법
-
번 원소가 속하는 집합의 번호
: 초기화는 각각 다른 숫자로 크기가 1인 n개의 집합을 만듦
- 합치기 연산은?
: 모든 원소를 순회하면서 한쪽 집합에 속한 원소들을 다른 집합으로 옮겨줘야함 =
너무 느려!
트리를 이용한 상호 배타적 집합의 표현
-
두 원소가 같은 트리에 속해 있는지 확인하는 방법 (Find)
: 각 원소가 포함된 트리의 루트를 찾은 뒤 같은 뒤 비교
- 모든 자식 노드가 부모에 대한 포인터를 가지고 있어야 함
-
두 원소가 포함된 집합 합치는 방법
: 각 트리의 루트를 찾은 뒤, 하나를 다른 한쪽의 자손으로 넣음
// 트리를 이용해 상호 배타적 집합 구현
struct NaiveDisjointSet {
vector<int> parent;
NaiveDisjointSet(int n): parent(n){ //init
for(int i=0; i<n; ++i){
parent[i]=i;
}
}
// u가 속한 트리의 루트의 번호를 반환
int find(int u) const {
if(u==parent[u]) return u;
return find(parent[u]);
}
// u가 속한 트리와 v가 속한 트리를 합침
void merge(int u, int v){
u=find(u); v=find(v);
if(u==v) return;
parent[u]=v;
}
}-
의 수행시간
: 해당 트리의 높이에 비례하는 시간
상호 배타적 집합의 최적화
트리가 한쪽으로 기울어지는 문제는 의 시간 복잡도를 유발
-
해결책
: 두 트리를 합칠 때 항상 높이가 더 낮은 트리를 더 높은 트리 밑에 집어넣음 (union-by-rank)
struct OptimizedDisjointSet{
vector<int> parent, rank;
OptimizedDisjointSet(int n) : parent(n), rank(n, 1){
for(int i=0; i<n; ++i){
parent[i]=i;
}
}
int find(int u) const {
if(u==parent[u]) return u;
return parent[u]=find(parent[u]); // 찾은 루트를 미리 바꿈으로 최적화
}
void merge(int u, int v){
u=find(u); v=find(v);
if(u==v) return;
if(rank[u]>rank[v]) swap(u, v);
parent[u]=v;
if(rank[u]==rank[v]) ++rank[v];
}
}-
합치기 연산과 찾기 연산의 시간 복잡도
:
- 찾기 연산의 최적화까지 적용되었다면 찾기 연산은 상수 시간에 작동한다고 볼 수 있음
: 우리가 상상할 수 있는 모든 크기의 에 대해 4 이하의 값을 가짐
Linking by Index / coin-flop linking
트리의 rank를 통해 최적화하는 방식은 rank를 저장할 공간을 요구한다. 그래서 저장 공간을 요구하지 않는 randomized algorithm이 존재한다. 이는 linking by index 를 통해 merge 연산을 최적화할 수 있다.
각 루트 값을 index를 통해 임의의 값으로 변환시킨다. 그리고 두 임의의 값을 비교하여 그 값이 작은 집합을 큰 집합에 붙인다.
void merge(int u, int v) {
u = find(u);
v = find(v);
if(u==v) return;
if(index[u] < index[v]) {
swap(u, v);
}
parent[v] = u;
}이는 그냥 동전 던져서 어디로 들어갈 지 정하는 솔루션과 시간복잡도가 같다고 오해할 수 있는데 사실이 아니다. 동전 던지기 솔루션의 시간복잡도는 으로 성능이 더 안좋다.
어떻게 가능하지.. 나중에 증명해볼 것
https://cp-algorithms.com/data_structures/disjoint_set_union.html
어디에 쓸까?
1. Connected components in a graph
굉장히 많이 쓰이는 경우이다.
정점 a, 정점 b가 같은 컴포넌트에 있는지 확인할 때 쓰인다. 유니온 파인드의 개념 자체를 사용하면 되므로 쉽게 풀 수 있다.
이 응용이 중요한 이유는 크루스칼 알고리즘으로 MST를 찾을 때 유니온 파인드를 통해 시간복잡도를 줄일 수 있기 때문이다.
2. Search for connected components in an image
한 이미지에 픽셀이 있다고 하자. 원래 이 픽셀들은 하얀 색인데 몇 개만 검정색이다. 알고 싶은 것은 이 이미지에서 하얀색인 컴포넌트의 개수이다.
이 문제는 DFS or BFS 로도 해결할 수 있지만 유니온 파인드로 푸는 장점이 있다. 유니온 파인드로 이 문제를 풀면 행렬을 행마다 처리할 수 있다. 이게 무슨 소린가?
유니온 파인드를 사용하면 연결 관계를 찾을 때 이전 행과 현재 행만 필요하다. 즉 메모리가 이 아니라 만 있으면 된다.
3. Store additional information for each set
유니온 파인드를 통해서 각 집합의 정보들을 쉽게 저장할 수 있다.
쉬운 예가 집합의 사이즈.
4. Compress jumps along a segment / Painting subarrays offline
유니온 파인드가 많이 쓰이는 또 다른 예이다. 정점의 집합이 있고 각 정점은 다른 정점으로 가는 단 하나의 간선을 가진다고 하자. 유니온 파인드가 있으면 시작점에서부터 모든 간선을 지난 도착점을 거의 상수시간에 알아낼 수 있다.
저 사실로 저 문제로 넘어간다고?
이 문제의 좋은 예가 problem of painting subarrays 이다. 길이 L 인 배열이 있고 각 원소는 0이다. 이제 subarray [l, r]를 색 c 로 색칠할 거고 이를 (l, r, c) 라고 하자. 구하고자 하는 것은 모든 색칠을 완료했을 때 각 원소의 색이다.
유니온 파인드로 이 문제를 풀려면 각 셀이 오른쪽에서 가장 인접한 색칠 되지 않은 셀을 가리키도록 해야된다. 밑의 그림에서 표현해보았다.
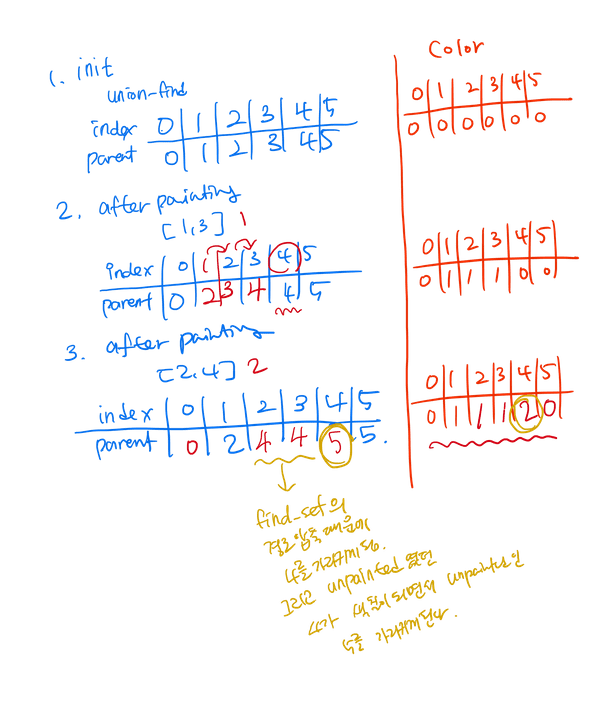
이제 문제를 풀어보자. 쿼리를 거꾸로 생각한다. 왜? 쿼리를 실행할 때 정확하게 subarray[l, r] 에서 색칠되지 않은 셀을 가리킬 수 있다. 다른 셀들은 이미 마지막 색깔로 나타내지니까.
경로압축으로만 최적화를 하고 rank를 사용한 최적화는 하지 않는다. 그러므로 머지할 때마다 시간복잡도는 이다.
for(int i=0; i<=L; ++i) {
make_set(i);
}
for(int i=m-1; i>=0; --i) {
int l = query[i].l;
int r = query[i].r;
int c = query[i].c;
for(int v = find_set(l); v<=r; v=find_set(v)) {
answer[v] = c;
parent[v] = v+1;
}
}만약 rank에 의한 최적화까지 한다면 다음 unpainted cell을 가리키는 end 배열을 추가로 사용해야 한다. 그렇게 하면 시간복잡도는 이다.
왜지!!
5. Support distances up to representations
한 정점과 그 그래프 (정점이 속한 집합)을 대표하는 정점과의 거리를 구하는데 사용할 수 있다.
경로 압축을 안쓰면 재귀적으로 거리를 구해야해서 비효율적이다. 경로 압축을 사용하면 각 노드에 부모까지의 거리를 추가적으로 저장함으로써 거리를 구할 수 있다.
void make_set(int v) {
parent[v] = {v, 0};
rank[v] = 0;
}
pair<int, int> find_set(int v) {
if(v!=parent[v].first) {
int len = parent[v].second;
parent[v] = find_set(parent[v].first);
parent[v].second += len;
}
return parent[v];
}
void union_sets(int a, int b) {
a = find_set(a).first;
b = find_set(b).first;
if(a!=b) {
if(rank[a]<rank[b])
swap(a, b);
parent[b] = {a, 1};
if(rank[a] == rank[b])
rank[a]++;
}
}6. Support the parity of the path length / Checking bipartiteness online
루트까지 길이를 저장하는 것처럼 루트 전의 경로 길이의 parity를 유지할 수 있다. 뭔소린지 모르겠음
7. Offline RMQ in on average / Arpa’s trick
배열 a[] 가 주어졌을 때 부분 배열에서 최솟값을 구해야한다.
유니온 파인드로 이걸 어떻게 해?
struct Query {
int L, R, idx;
};
vector<int> answer;
vector<vector<Query>> container;
stack<int> s;
for (int i=0; i<n; ++i) {
while(!s.empty() && a[s.top] > a[i]) {
parent[s.top()] = i;
s.pop();
}
s.push(i);
for (Query q:container[i]) {
answer[q.idx] = a[find_set(q.L)];
}
}이 접근 방법은 오프라인으로만 작동한다. 즉, 모든 쿼리를 미리 알고 있어야 한다.
8. Offline LCA in on average
9. Storing the Union Find explicitly in a set list / Applications of this idea when merging various data structures
10. Storing the Union Find by maintaing a clear tree structure / Online bridge finding in on average
https://cp-algorithms.com/graph/bridge-searching-online.html
![[jungin]](/static/035ce7483ee8f639767376dfc414c0e6/f4007/profile.png)