코드포스 Animals and Puzzle
문제
풀이
Editorial을 보면 문제의 핵심을 3가지로 요약할 수 있다.
1. DP
어떤 구간에서 정사각형의 최대 길이를 어떻게 알 수 있을까?
임의의 구간을 생각하기 전에 먼저 한 점이 고정된 구간을 생각해보자. 2차원 배열에서 A[i][j] 를 포함하는 (여기서 포함한다는 뜻은 무조건 A[i][j] 가 1이어야 함을 뜻한다) 최대 정사각형의 길이는 다음의 식으로 표현할 수 있다.
2. Sparse Table
이제 DP에서 구한 값을 이용하여 Sparset Table st 를 구성하자.
- 2d sparse table 구하기
for (int i = 0; i < LOGN; ++i) {
for (int j = 0; j < LOGN; ++j) {
for (int r = 0; r + (1 << i) <= n; ++r) {
for (int c = 0; c + (1 << j) <= m; ++c) {
if (i == 0 && j == 0)
continue;
if (i == 0) {
st[r][c][i][j] = max(st[r][c][i][j - 1], st[r][c + (1 << (j - 1))][i][j - 1]);
} else if (j == 0) {
st[r][c][i][j] = max(st[r][c][i - 1][j], st[r + (1 << (i - 1))][c][i - 1][j]);
} else {
st[r][c][i][j] = max({st[r][c][i - 1][j - 1], st[r + (1 << (i - 1))][c][i - 1][j - 1],
st[r][c + (1 << (j - 1))][i - 1][j - 1],
st[r + (1 << (i - 1))][c + (1 << (j - 1))][i - 1][j - 1]});
}
}
}
}
}query(l, r)
int query(int x1, int y1, int x2, int y2) {
int dist1 = LOG[x2 - x1 + 1], dist2 = LOG[y2 - y1 + 1];
return max({st[x1][y1][dist1][dist2], st[x2 - (1 << dist1) + 1][y1][dist1][dist2],
st[x1][y2-(1<<dist2)+1][dist1][dist2], st[x2-(1<<dist1)+1][y2-(1<<dist2)+1][dist1][dist2]});
}3. Binary Search
마지막 단계인 이분 탐색이다. 이제 주어진 쿼리에 대해서 구간 내에 가장 큰 정사각형의 길이를 반환해아한다.
어떻게? 앞에서 구한 것으로 다 해결되었다.
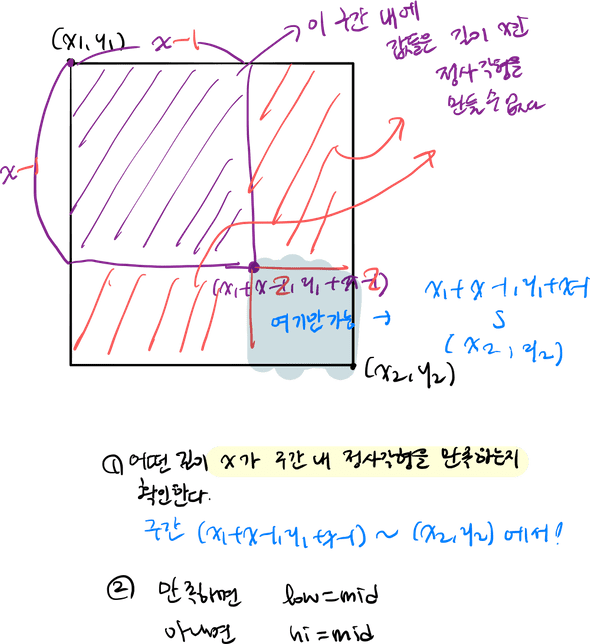
int binarySearch(int x1, int y1, int x2, int y2) {
int low = 0, high = min(x2 - x1 + 1, y2 - y1 + 1);
int ans = 0;
while (low <= high) {
int mid = (low + high) / 2;
if (compute(x1, y1, x2, y2, mid)) {
ans = mid;
low = mid + 1;
} else
high = mid - 1;
}
return ans;
}